Constructing High-Level Symbolic Representations for Planning

Our research in this area addresses a core question at the heart of intelligent robotics: how should robots construct abstractions that are simultaneously rich enough to support planning, and impoverished enough to make it efficient?

Robots, like humans, interact with the world through low-level action and perception. While everything the robot does must eventually be realized using pixel-level sensing and motor-level action, intelligent decision-making at that low level is hopelessly complex. When you decide to travel from one city to another, you cannot possibly construct a plan that describes a long sequence of muscle contractions that you plan to take, and that anticipates the gigabytes of image data that you expect to pass through your retinas on the way. Instead, you reason using very high-level actions (e.g., take a taxi to the aiport) and very high-level abstractions of state ("I'm at the airport"), and fill in the details on the fly.

A robot that could do the same would be capable of generating much more intelligent behavior than even the most complex existing systems. But robots don't get the representations that support abstract reasoning from the environment; they must either rely on a designer (which only works for special-purpose, task-specific robots), or generate them for themselves. While hierarchical reinforcement learning has focused on the problem of learning and using higher-level motor skills (which allow the robot to abstract its actions) much less attention has been paid to the complementary problem of abstracting the robot's state.

Our approach is to construct such abstractions from the bottom up, grounding them in the real sensorimotor actions of the robot, while ensuring that they support, by construction, the reasoning required for their purpose. We formalize the queries that the representation must support to determine the types of mathematical objects it must contain, and which instances of those objects must be present in a representation to support planning:

• For deterministic planning, the relevant mathematical objects are sets, so we construct a representation where symbols are grounded by sets of low-level states. (This corresponds to the classical semantics for propositional symbols.) We describe the collection of sets that is necessary and sufficient for planning and, when that collection is finite (which depends on properties of the motor skills), show how to build a sound and complete model using them. The grounding sets can then be discarded for the purposes of planning; only the abstract model is necessary.

• For probabilistic planning, symbols must be generalized from referring to states to referring to distributions. Again we show how to construct the relevant distributions to form a complete symbolic vocabulary for planning using the robot's skills, and show how to use them to construct an abstract probabilistic model, suitable for planning. In addition, we show how to apply the well-studied problems of density estimation and probabilistic classification to autonomously learn the relevant grounding distributions.

The image below shows an experiment where a robot is placed in a room with a cupboard, cooler, switch, and green bottle. The robot's task was to learn an abstract model of the room and use it to plan on demand, using a collection of pre-programmed motor controllers (e.g., for moving between the cooler and cupboard, and opening and closing each). The room contained several implicit logical dependencies (e.g., the robot could only open the cupboard or cooler when both grippers are empty; when the switch is on it illuminates the inside of the cupboard, preventing the robot from picking up the bottle if it is inside). However, these dependencies are not given to the robot - it must discover them, and the symbolic vocabulary necessary to describe them, using only its own experience and raw sensorimotor data.

Photos taken during our experiment. On the left, the cooler is open and the robot has picked up the green bottle. On the right, the bottle has been placed in the open cupboard. Note that the robot's left arm is lowered when its gripper is empty, and raised when it is holding the bottle.

Our framework enabled the robot to learn an abstract symbolic representation of the environment. That representation consists of operator rules, which describes the conditions under which a motor skill can be executed, the effect of doing so, and the average cost (in our case execution time). The symbols used to describe these operator rules, as well as the rules themselves, are discovered autonomously by the robot. Below we show one such rule - for opening the cupboard - along with visualizations of each symbol's grounding distribution.

symbol1	symbol3	symbol4	symbol5

The operator describing the motor skill for opening the cupboard (top), and visualizations (via sampling) of the relevant symbol grounding distributions (bottom row). The skill can only be executed when symbols 1, 3, and 4 are true. Symbol 1 grounds to a distribution over the robot's location in the map, indicating that it is in front of, and facing, the cupboard. Symbol 3 is a distribution over the robot's joint poses, indicating that both arms are lowered (and hence both grippers are free). Symbol 4 is a distribution over the voxels making up the cupboard, and can be interpeted as the cupboard door being open. Execution of the skill causes symbol 4 to become false, and symbol 5 (also a distribution over cupboard voxels, indicating that the cupboard door is open) to become true. Skill execution takes approximately 64 seconds. The operator therefore expresses the knowledge that, in order to open the cupboard door, the robot should be standing in front of it, not holding anything, and the door should be closed. Afterwards, the door will be open instead of closed.

The operator below describes the motor skill of opening the cooler, which has a stochastic outcome: some of the time, when the robot pushes the cooler top open, it bounces shut again.

symbol0	symbol3	symbol8	symbol9

The operator describing the skill for opening the cooler (top) and visualizations (via sampling) of the relevant symbol groundings (bottom row). The skill requires symbols 0, 3, and 9 to be true, which indicate that the robot is standing near and facing the cooler, with both grippers free, and that the cooler is closed. The operator has a stochastic outcome: most of the time, symbol 9 becomes false and symbol 8 (indicating that the cooler is open) becomes true. However, approximately 8% of the time, the cooler lid bounces back closed, resulting in no state changes.

The abstract representation learned above is sound and complete for planning, and is suitable for input to an off-the-shelf planner. The grounding distributions are not required once the model has been built. Planning to move the bottle from the cupboard to the cooler took only about 4ms using the abstract representation. A video describing our approach, showing the robot learning, describing the resulting representation, and demonstrating planning, can be viewed below.

The primary results of our work are that:

• A collection of motor skills uniquely specifies the appropriate symbolic representation for planning (procedural abstraction drives perceptual abstraction).
• A principled framework for constructing the appropriate symbolic representation now exists.
• Probabilistic planning requires generalizing the semantics of a propositional symbol from a name for a set (the classical semantics) to a name for a distribution.
• The appropriate representation can be autonomously learned by a robot.

Our work is described in the following journal paper:

• G.D. Konidaris, L.P. Kaelbling, and T. Lozano-Perez. From Skills to Symbols: Learning Symbolic Representations for Abstract High-Level Planning. Journal of Artificial Intelligence Research 61, pages 215-289, January 2018.

The above paper supercedes two earlier conference papers:

• G.D. Konidaris, L.P. Kaelbling, and T. Lozano-Perez. Symbol Acquisition for Probabilistic High-Level Planning. In Proceedings of the Twenty Fourth International Joint Conference on Artificial Intelligence, pages 3619-3627, July 2015.
  
  
• G.D. Konidaris, L. Kaelbling and T. Lozano-Perez. Constructing Symbolic Representations for High-Level Planning. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, pages 1932-1940, July 2014.

The above research was supported a by DARPA Young Faculty Award.

An immediate consequence of our results is that state procedural abstraction are complementary, but that procedural abstraction drives state abstraction. In fact, these two processes can be alternated to form a skill-symbol loop: skill acquisition creates skills, which provide the opportunity to construct a new, abstract, decision problem, which skill acquisition can be applied to in turn. Our research on this approach is still in its early phases, but some initial results on the Taxi problem are shown below.

       

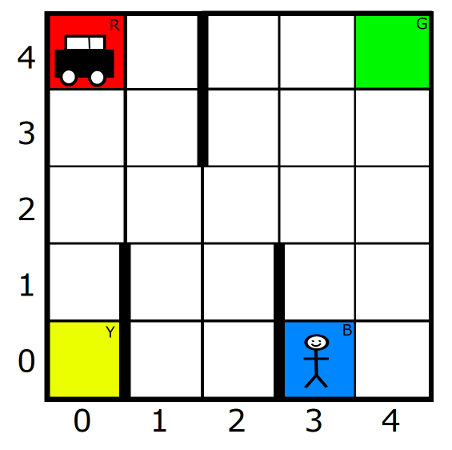
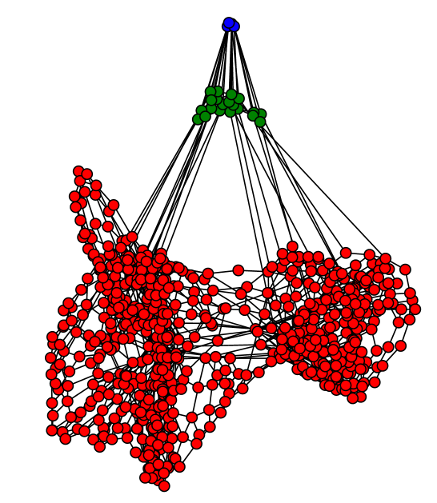
The Taxi domain (left), a standard hierarchical reinforcement learning benchmark, and a hierarchy of increasingly abstract task representations (right) constructed by alternating skill- and representation-construction phases. The hierarchy enables planning for common tasks in less than 1ms.

Our work on building hierarchies of representations can be found in the following paper:

• G.D. Konidaris. Constructing Abstraction Hierarchies Using a Skill-Symbol Loop. In Proceedings of the 25th International Joint Conference on Artificial Intelligence, July 2016.